Виктор Фесенко - Невозможные объекты. Классификация и примеры
НО типа D
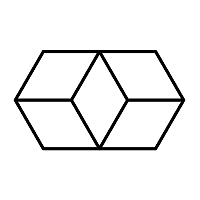
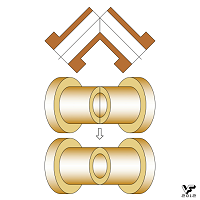
В 1895 году Арманд Тьерри придумал необычную геометрическую конструкцию, которую назвали его именем:
VII
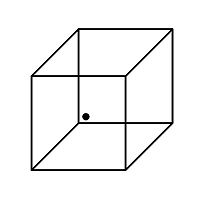
Эта фигура состоит из двух кубов: верхнего с просматриваемой нижней гранью и нижнего с просматриваемой верхней гранью. Вся прелесть фигуры Тьерри заключается в том, что эти просматриваемые грани обоих кубов представляют собой одну и ту же поверхность, т.е. кубы срослись друг с другом похлестче сиамских близнецов. Предлагаемая автором классификация относит кубы Тьерри к НО типа D, основным свойством которых является двоякое зрительное восприятие некоторых геометрических объектов и их фрагментов. На данное свойство еще в 1832 г. впервые обратил внимание некий Нэкер, предложивший интересующейся публике порассуждать о точке, изображенной на фоне нарисованного решетчатого куба:
VIII
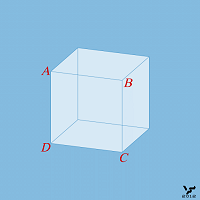
Читателям предлагается ответить: как черная точка расположена относительно куба, перед ним, внутри или позади него. Куб Нэкера допускает равноценное существование всех трех версий расположения. Аналогичный случай неоднозначности взаиморасположения нарисованных геометрических объектов можно констатировать и при созерцании монолитного стеклянного (прозрачного куба) с нулевым углом преломления световых лучей, показанного на Фиг. 107. Два наблюдателя могут воспринимать его по-разному: один будет утверждать, что грань с вершинами A, B, C и D является у куба фасадной, а другой назовет ее тыльной, проглядывающейся через толщу стекла. И оба наблюдателя будут правы.
107
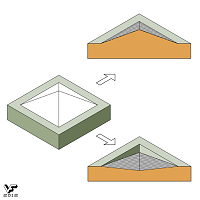
Примером такой же неоднозначности зрительного восприятия может быть вполне возможная конструкция, изображенная на Фиг. 108:
108
Рисунок не может дать четкий ответ на вопрос: какую форму имеет изображенная фигура, то ли это толстая квадратная плита с выступающей на ее верхней поверхности четырехгранной правильной пирамидой, то ли это та же плита, но с четырехгранной несимметричной выемкой.
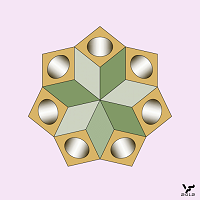
В фигуре Тьерри невозможным образом срослись только два куба (параллелепипеда), но количество сросшихся фигур может быть большим:
109
110
111
Фигурами Тьерри могу выступать не только интегрированные параллелепипеды, а и разнообразные тела вращения:
112
113
114
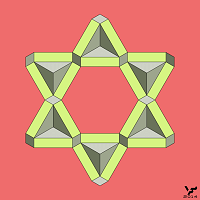
И не только тела вращения. На Фиг. 115 – 120 приведены примеры других НО типа D:
115
116
117
118
119
120
По типу сросшихся кубов Тьерри можно объединить корешки двух книг:
121
122
А что изображено на Фиг. 123 - два дома с пятиугольным двориком между ними или три дома со сросшимися стенами и скатами крыши, судить читателям:
123
Весьма интересным и забавным невозможным объектом типа D является симбиоз балкона и террасы на картине Девида Макдональда:
IX
В Интернете отыщется несколько изображений НО типа D, выполненных способом редактирования и совмещения фотографий, таких, как невозможный перекресток художника Эрика Джоханссона:
X