Виктор Фесенко - Невозможные объекты. Классификация и примеры
НО типа A
Многие из нас видели фотографии, выполненные в туристических поездках, на которых один путешественник удерживает на ладони вытянутой руки или знаменитое архитектурное сооружение или, стоя на фоне большой лестницы, своего товарища по путешествию:
002
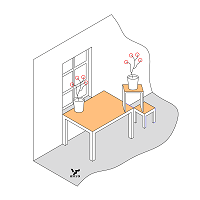
Технология выполнения таких фотоснимков настолько проста, что не требует разъяснения. Подобные ухищрения и используют авторы НО типа А, объединяя (совмещая) на рисунке такие поверхности, линии, грани или оси, которые в реальной ситуации разнесены в пространстве друг относительно друга, но находятся на одном и том же направлении взгляда. На Фиг. 003 приведен простой и наглядный пример НО типа A :
003
Верхние поверхности обеденного стола и табурета никак не могут принадлежать одной горизонтальной плоскости, если эти предметы мебели имеют общепринятые средние размеры и находятся на общем горизонтальном полу. А художник может себе позволить изобразить одновременно на столе и табурете подставку с цветочным горшком.
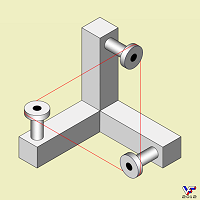
Самым известным из всех ранее созданных НО является треугольник, образованный тремя взаимоортогональными стержнями квадратного сечения, который в 1954 г. предложили миру Роджер и Лайонел Пенроузы, опубликовав в Британском журнале психологии статью о невозможных фигурах. А хронологически первым НО является фигура, подобная треугольнику Пенроуза, нарисованная в 1934 г. Оскаром Реутерсвардом и в которой вместо трех взаимоортогональных стержней были изображены расположенные на трех осях кубики:
V
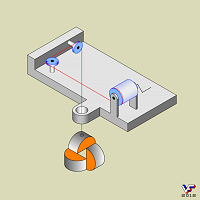
Три взаимоортогональные оси, на которые нанизаны кубики, также, как и стержни в фигуре Пенроуза, образуют геометрически невозможный равносторонний треугольник. На Фиг. 004 проиллюстрирован один из видов генезиса треугольника Пенроуза:
004
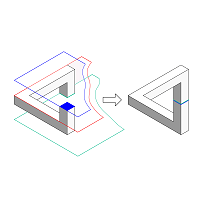
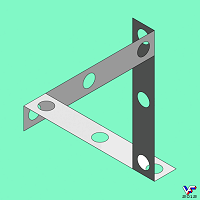
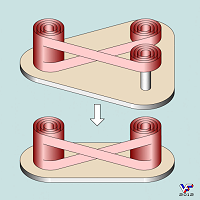
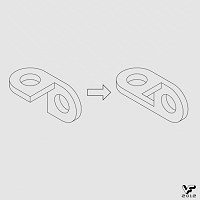
На Фиг. 005 показано, что треугольник Пенроуза может быть получен не только невозможным для реального мира соединением трех стержней своими концами, а и соединением трех Г-образных фигур. На этом же рисунке показано типовое родство треугольника с невозможным кольцом, образованным невозможной интеграцией трех дугообразных фигур:
005
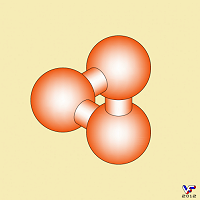
Более того, треугольник Пенроуза или его кольцевая разновидность могут образовываться из трех прямолинейных или дугообразных элементов круглого сечения:
006
007
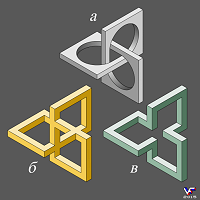
На Фиг. 008 – 017 можно увидеть родных и двоюрдных братьев треугольника Пенроуза, полученных также невозможной интеграцией трех одинаковых элементов, сама форма интегрируемых элементов может быть весьма разнообразной в т.ч. и по пространственной размерности:
008
009
010
011
012
013
014
015
016
017
Для треугольника Пенроуза и его аналогов существует их предельная конфигурация, при которой три интегрированных элемента максимально приближены друг к другу:
018
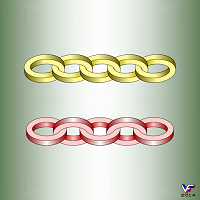
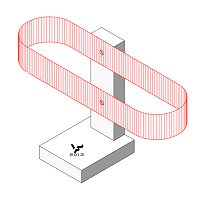
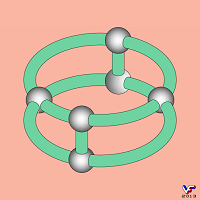
Немного менее известным, но не менее изящным представителем НО типа A является Невозможное кольцо, один из вариантов генезиса которого показан на Фиг. 019:
019
По имеющейся в Интернете информации, это необычное кольцо было придумано Дональдом Е. Симанеком и независимо от него разработано для эмблемы фирмы Canstar, производящей оптоволокно. Возможно также, у этого НО есть и другие авторы.
Родственников Невозможного кольца можно напридумывать немало, например таких, как на Фиг. 020 - 027:
020
021
022
023
024
025
026
027
Судя по всем предыдущим публикациям, подавляющее количество ранее созданных НО можно отнести к типу A, причем основную долю среди них составляют многочисленные вариации т.н. мультибаров – пространственных структур, состоящих из различного количества стержней квадратного или прямоугольного сечения. Может быть это и не плохо, но отыскать среди их сотен что-нибудь новенькое, в смысле идей НО, бывает порой трудоемко. По этой причине автор своими собственными рисунками НО типа A не стремился увеличить количество вариаций невозможных мультибаров.
На Фиг. 028 – 029 представлены одномерные НО типа A, построенные в изометрической проекции:
028
029
На Фиг. 030 – 032 представлены двухмерные НО типа A также в изометрических проекциях:
030
031
032
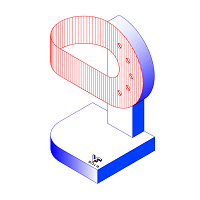
На Фиг. 033 изображена в изометрической проекции одна невозможных версий листа Мебиуса – односторонней поверхности в виде замкнутой ленты:
033
На Фиг. 034 – 042 в изометрических проекциях проиллюстрировано многообразие трехмерных НО типа A:
034
035
036
037
038
039
040
041
042
Дополнительные идеи при поиске новых НО возникают при их представлении в одноточечной или двухточечной перспективе:
043
044
045
046
047
048
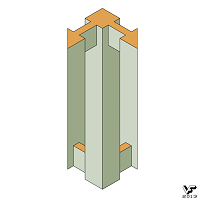
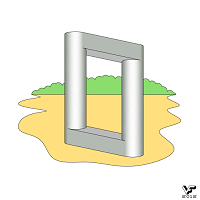
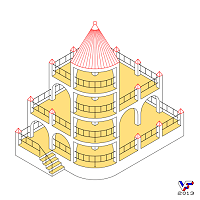
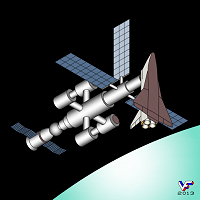
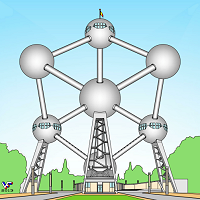
Большое внешнее однообразие НО, состоящих из разного количества брусков, колец или рамок несколько утомляет и вниманию читателей предлагается серия НО типа А, нарисованных в виде зданий и сооружений различной формы, среди которых многоэтажные дома с сотней окон, постройки с внешними лестницами, воображаемое блуждание по которым приводит к пространственному парадоксу, многоэтажные сооружения, любой этаж которых можно посетить без помощи лестниц, другие объекты архитектуры или техники:
049
050
051
052
053
054
055
056
057
058
059
060
061
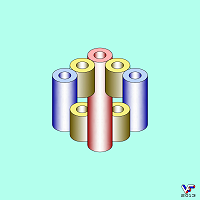
Как отмечалось ранее, невозможной может предлагаться не только интеграция (соединение) геометрических структур или их частей, а и просто их взаиморасположение друг относительно друга, как проиллюстрировано на Фиг. 062 – 064:
062
063
064