M.C.Escher's Legacy. A Centennial Celebration
Organic Structures Related to M.C. Escher's Work
Escher as Inspiration for Research
M.C. Escher interpreted three-dimensional spatial structure with the help of the living world - fauna, flora and human figures. His spatial forms behave in a unique way: they appear to be realistic, but they cannot be constructed in the real three-dimensional world. This visual phenomenon, illusion in the plane, was approached from different viewpoints by Escher. In representing spatial structures Escher utilized the Penrose triangle and the Möbius band. I have dealt with representing these "organic" forms in the plane, defining rules for organization of basic structures. Designing and experimenting with such organic structures has become an especially exciting field for basic research.
Here I introduce the basic principles that may help you recognize and understand the different areas of my investigations. I have defined five main fields of inquiry that intersect with art and science.
- Continuous stereoscopic configurations. These are generally prismatic figures intersected by a square. These occur in M.C. Escher's prints Möbius Strip I [1, cat. no. 298] and Möbius strip II, and Waterfall.
- Visual and logical relationships between stereoscopic configurations; organizing modular systems into adjacent figures. Examples are given by M.C. Escher's prints Stars [1, cat. no. 359] and Belvedere.
- Visual and logical organizations of stereoscopic formations usually created from cubes or short prismatic units such as in M.C. Escher's print Cycle.
- Organization of stereoscopic figures into systems similar to stairways as in M.C. Escher's print Ascending and Descending.
- Symmetrically recurring plane and stereoscopic formations filling the plane and space. (These configurations may be multiplied in all directions of the space, filling the surface accordingly.) M.C. Escher's print Metamorphose II is an example.
My Spatial Art
I have been concerned with researching and making artistic presentations of strange stereoscopic configurations since 1972. To date, I have designed about 1,500-2,000 impossible forms.
The main direction of this research is developing the so-called continuous stereoscopic configurations of type 1. Their primary characteristic is that one, two, or three lines form the structure. The line describes a recursive spatial path in the plane. The rectangular prism looks real, and usually moves in all directions of the given space, in 90° steps. The viewer can comprehend the movement of spatial structure in the picture series Celtic XII 96 (Fig. 1, left). Forms follow each other playfully underneath and above. Similar rules describe the structure of Celtic VIII 96 (Fig. 1, right, and color plate 28), where a star-structure becomes a continuing spatial formation. Here the stream is also a self-recurring one. In some places within the form, the configurations cover each other in short sections, but they do not cross one another or join each other. Many of them are organized on a hexagonal grid, while even more follow a triangular or rectangular net.

In works of type 2, the stereoscopic configurations diverge, cross, and connect with each other. Lateral faces appear simultaneously; usually the cubes or prismatic parts connect to each other, creating an impossible figure. They appear on a hexagonal net, but they also exist on triangular or rectangular nets. If we start from the center of Atlantis VI 86 (Fig. 2, left), we perceive the space in all directions. The joining of the cube-like formation is not real, and that is why we discover six projections of it. The effect of Magical Space 86 (Fig. 2 right) is like revolving a frame from one view to another.

Stereoscopic configurations, cubes and prisms create a unified system by touching each other or merging into one another in works of type 3. The basis of structures originating in this manner is determined with a special spiral or circle. The spiral could have one, two, three, or even six arms. In these works, one may discover several lateral faces simultaneously. Cubes are compressed in a special way in Crystal-M 18/86 (Fig. 3, left), creating an unreal three-dimensional formation, as they grow out from each other. Here, one can discover six frontal views, or a spiral track of a crystal-like construction.
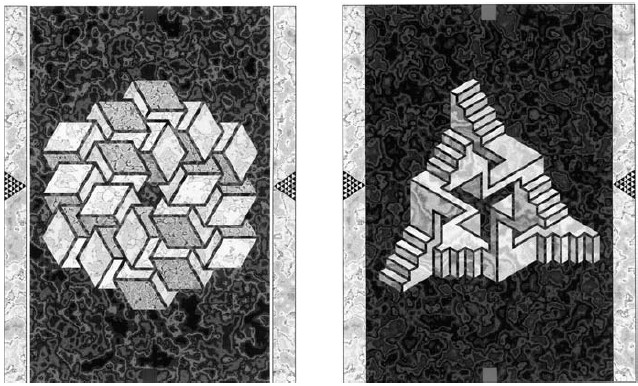
More complex stairway figures usually organize themselves into one system in works of type 4. We may either go round on the steps of these stereoscopic configurations, or move forward to the center. Pyramid 97 (Fig. 3, right) contains three Penrose triangles which are combined with an impossible staircase construction. If we go around the outside of the structure, we don't feel its unreality - it looks like a "buildable" form, but trying to get to the center provides the disappointment of three-dimensional reality.
In works of type 5, we find repetition of plane or stereoscopic configurations on the surface. The plane figures are generally situated so as to be equidistant from one another. One form may repeat itself, or three of them may create a basic system in which the forms traverse each other. The stereoscopic figures are able to cause similar effects. The system can continue in all directions to fill a twodimensional plane in a regular and symmetric manner. Therefore, the system is continuable and expandable to infinity. The form of the figures can differ several times, and so we can discover one, two, or three forms within one system. Dynamic Pattern II 90 (Fig. 4) can be "read" in many ways.

We owe deep thanks to M.C. Escher for opening the gate to an extremely exciting and varied world, and enlarging the borders of visual perception with his work.
Reference
- F.H. Bool, J.R. Kist, J.L. Locher, F. Wierda, eds., M.C. Escher, His Life and Complete Graphic Work, Harry Abrams, New York, 1982.
